Mission Report: Year 2

When I started writing this blog, one of my hopes was to each year write an end-of-year summary of what I’ve been up to. My semester ended a few weeks ago, though, and I’m only getting around to writing this reflection now because for the past week and a half I’ve been in Houston, Texas at a graduate summer school in dynamical systems. So that explains why I’ve been a little poky on writing this particular post.

It doesn’t explain why I’ve been AWOL on this blog in general this year, though. The last thing I wrote was my open letter to a priest at Penn State on his conspicuous silence regarding the Women’s March on Washington. Before that, the last thing I’d written was an explanation on how I reconcile my spirituality with my faith in the scientific method—in July. So yeah, I’ve been slacking. In the Fall, the reason for this was I’d been really stressed out about qualifying exams, and almost all of my energy was devoted to preparing for my final qual in linear algebra (which I passed in December, thankfully).

Unfortunately, for a period of time in the beginning of the Spring, I realized I’d almost burned myself out studying for qualifying exams. I’d moved on to studying more specific and advanced topics pertinent to my research interests, but I’d become badly self-critical when I failed to solve a problem or understand a particular concept. I tell my students that making mistakes in mathematics is a good thing, because when you make a mistake, you have the opportunity to learn a new way of thinking you hadn’t experienced before; our comprehension grows when we discover we screw up and find ways of correcting ourselves. Twistedly, I was having trouble following my own advice for much of this semester.

Without getting into the dark and disturbing details, I’ve been dealing with a few different forms of self-doubt this semester. A lot of it boiled down to me asking myself, “Why am I still pursuing mathematics as a career?” Consequentially, this semester has involved a number of existential quandaries and crises of faith. (But hey, I don't think I'm the only grad student to feel this way in their second year.) I still think it's important for me to write these posts though, because (a) I still feel compelled to attempt to express why I find mathematics beautiful, even if it devolves into me shouting into the void occasionally; and (b) I want to hold myself accountable for my different spiritual and theological positions.

Despite these new challenges, this has been an exciting year in many ways! I have a PhD advisor now, for one thing, and with that a research direction. I’ve entered into the sub-community of mathematicians studying dynamical systems. I taught the same course in both the Fall and Spring semesters and got to know some terrific engineering and science undergraduates in the process. I took some exciting math courses in both semesters and read through John Lee’s book on smooth manifolds, which was one of my New Year’s resolutions. (And you know, smooth manifolds made SO much more sense after studying it a second time, so that’s something!)

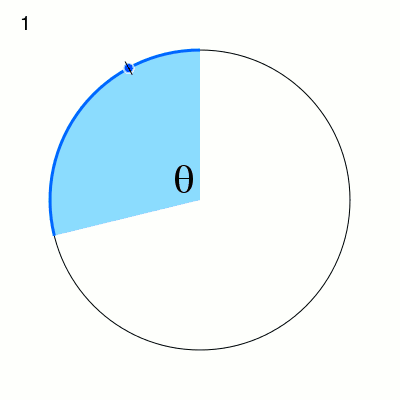
So my general area is dynamics. Loosely speaking, a dynamical system is a universe with a way of measuring distance, along with a rule dictating how points in this space move. The simplest example of a dynamical system I know of is circle rotation. Here, the universe is a circle (specifically the edge of the circle), and the rule is that each point movies counterclockwise by some fixed angle. Dynamists ask questions like, “What happens if you apply the rule to the point several times? What if we apply the rule once, then apply the rule to this new point, then again to the next new point, then again, then again, and on and on?” If we do this, we get what’s called the “orbit” of the point. The question we often ask is, “What does the orbit look like?” In some cases, we find that the points in the space get closer and closer to each other the more you apply the rule. (The image to the left shows the first few iterates of a circle rotation by an irrational angle, a famous class of dynamical systems. The different ticks on the circle are the orbit.)

As the second example, suppose your system is a 2-dimensional disc, and your rule is the distance of each point from the center gets cut in half. Then each point gets closer and closer to the center the more you apply the rule. This is called a “contraction map”, because the circle contracts. The center of the circle is called a "fixed point", because the point is fixed by the rule of the system. (Mathematics is nothing if not descriptive.)

Now, contraction maps and rotations are very well behaved and easy to study. A more difficult system to study is the weather. Even very simple models of the weather have incredibly sophisticated dynamics; in fact, this is the beginning of the area of mathematics now known as chaos theory, where two points that are close together go on to behave very differently after a certain amount of time. The famous image of the Lorenz butterfly (below) comes from the orbits of an early 3-variable weather model, the first discovered example of a chaotic continuous system.

The kinds of systems I study are systems that not only have distance between points, but also have a notion of volume of subsets. Specifically, all my universes have volume 1; this is what’s often called a “probability space”, where subsets of the space are thought of as probabilistic events. The rule on the space shows how one probabilistic event changes to another probabilistic event. The study of dynamics on these kinds of spaces is known as “ergodic theory”. Ergodic theory in and of itself is an incredibly rich field, and countless results from statistics, number theory, and mathematical modeling come from ergodic theory. Including, in particular, the purely mathematical definition of entropy.

Entropy is typically thought of as a “measurement of disorder”; greater entropy implies greater disorder, and in thermodynamics we observe that the universe tends towards greater entropy, or greater disorder. (When you drop some food coloring in water, it disperses and diffuses throughout the water; you do not see it take the shape of Michelangelo’s David in the water, because this would be a highly ordered, very low-entropy state.) You can also think of entropy as a measurement of how much information you get about a large system by looking at a small sample. The sequence of coin tosses HTHTHTHTHT…, for example, has very low entropy: if you look at two consecutive characters in the string, you have an accurate view of the entire string. However, the sequence of coin tosses HTTHHTHTHHTTTTTHHHTHHH… has very high entropy, because even a very large section—like the one we’ve written—tells us very little information about the overall sequence. (If you gamble with coin tossing, and you see the sequence HTHTHTHT… appear in your gambling, you would reasonably be very suspicious of this coin!)

My research involves determining and classifying the thermodynamic properties—entropy, for example—of ergodic dynamical systems whose thermodynamics have not yet been thoroughly investigated. At this point in my career, however, I’m producing very few original results; I’m mostly reading background material to understand more about the specific dynamical system whose thermodynamics I’m investigating.

(Full disclosure: I haven’t defined what an “ergodic dynamical system” is yet, only what “ergodic theory” concerns itself with; and I certainly haven’t described the kind of system I’m investigating, because they require basic knowledge of Riemannian geometry to meaningfully define. I have a suspicion my family and friends reading this have had enough of the math lessons at this point.)

In addition to my research, I’ve now gone to a couple conferences and workshops on dynamics and geometry. I’ve been to two notable ones in particular: a weekend conference at the University of Maryland (UMD and Penn State share two dynamics conferences a year: the Fall conference is at Penn State and the Spring conference is at UMD), and a summer workshop on dynamics at the University of Houston. What I learned at both of these conferences is that the field of dynamics is a truly immense research area. What I study is smooth ergodic theory; others study partial differential equations, others study what’s called “complex dynamics” (from which we get such gems as the Julia and Mandelbrot sets, see below), others study the applications of dynamics to number theory, and still others study stochastic processes (modern chaos theory). And that barely scratches the surface of what areas of mathematics dynamical systems touches on. So the field of dynamics requires you to know a little bit of everything from different math subjects. Even then, after years of experience, you could go to a conference on dynamics and still be confused by several of the talks. So even though I can tell how much I’ve learned over the course of this past year, in a very real way, it never feels like enough.

The temptation that I’m constantly faced with is putting my research on the backburner, and instead reading and solving problems from textbooks on ergodic theory, differentiable manifolds, Riemannian geometry, and algebraic topology. These are all fields that are relevant to not only my research specifically, but to dynamics as a whole, and plus the results and problems that come out of these subjects are really incredible. (The first chapter of my algebraic topology textbook proves, for example, that at any given moment, there are two opposite points on the surface of the Earth that have the exact same temperature and barometric pressure. Weird, right?)

Besides being fascinating in its own right, a big reason focusing on the basics is tempting is because research is really difficult. Easily the most difficult thing I’ll ever have done in my life. (And yes, I know I said that last year.) On the one hand, reading textbooks on abstract geometry and topology is fun and relatively simple, but of course it’s all been done before. On the other, research is exciting and adventurous, and I can’t wait to get my hands dirty working on problems no one has solved before, but it’s really friggin’ hard. So it helps to break up my work by alternating between two kinds of mathematics: the easier kind that I can figure out on my own relatively easily (textbooks on abstract geometry and topology), and the really hard kind that no one has done yet but I just might.

But what I’ve begun to find is that no matter how many problems I do, or how many textbook chapters I read, there will still be more background subjects for dynamics that I could study next, and I’d never get around to doing my own research. Learning math is fun, but that can’t be all that I do, even if it’s ostensibly to prepare myself for research. Realistically, I’ll never be “prepared enough”. It’s time for me to stop only doing background reading and actually try to produce some original results.

Geronimo.