Mission Report: Year 1
- dveconi

- Jun 10, 2016
- 9 min read
And so my first year of graduate school comes to a close! Well actually it came to a close a few weeks ago, and I’ve just been lazy since then, but I’ve been meaning to write a brief reflection on my first year in the Penn State mathematics Ph.D. program. Why have I waited so long to write it? Because apparently procrastination is one habit I never outgrew. Oh well.
I can say without exaggeration that all in all, this past year has been probably the single biggest challenge I’ve ever faced in my life. Not the most difficult period of my life, but certainly the greatest challenge. I’ve never been busier day to day than I have been this past year. One way that graduate work is different from undergrad work is that assignments and due dates don’t carry the same weight. You have assignments, and they have due dates, but many professors are very generous with extensions, especially if you really want to have an answer for each of the different problems (in several cases, you might just skip a number of the problems and no one bats an eye). I had one course last semester that ended up only having two assignments and no other work during the entire semester, and the second assignment I barely scraped by understanding, let alone knew how to answer most of the problems. I still got an A in the class. Consequence: GPA matters basically zip when you’re a grad student.
So what keeps me busy isn’t the assignments. It’s the out-of-class learning. Compared to undergrad, your professors do a much smaller fraction of the work for you when it comes to learning the material. Predominantly, you have to teach yourself. You might ask them some clarifying questions, but you’re more or less on your own. That applies during all stages of the program, whether you’re actively researching, or still working on qualifying exams (more on that later). Seemingly every night this past year I’d go to sleep thinking,
“Yeah, I did good work today. I made progress on stuff. But I could have done one more problem. I could have thought about this for a little bit longer.”
I have a few friends who are current undergrads in mathematics thinking about going on to graduate school. I made this comparison to one of them:
“Being a mathematics grad student in your first year is like being a kid in a candy store. You never thought you could be exposed to this much math in so little time, and you just want to do it all. You want to try all of it. You feel like you can’t get enough of it, but eventually your parents have to drag you out of the candy store kicking and screaming. Only here, your parents are your body telling you that you need to eat and sleep.”

Seriously though, my parents often ask me how I’m doing when it comes to cooking for myself. My problem is, I’ll get so wrapped up in something that I’m working on, I’ll completely lose track of time. I get back to my apartment, unpack my bag, maybe grab some coffee from the lobby of the complex’s main building, and get straight to work. Before I know it, it’s 8:30 or 9:00 at night, and I think, “Meh, I guess I should eat something.” So I whip together something horrifyingly quick and simple, often macaroni and cheese with salsa, tuna, peppers and onions, or something else. None of this bothers me when I’m at PSU, but after being back home for a couple weeks, I’m realizing how badly I missed good food. But that’s what happens when your budget (in terms of both time and money) is as tight as your typical grad student. (For those of you who don’t know my family, my parents are HUGE foodies. My dad especially will cook some of the most unbelievable things out of Jacques Pepin or Julia Child’s cookbooks. So they probably wouldn’t touch what I cook for dinner with a 10-foot pole.)
But hey, I wouldn’t change this for the world. I’ve absolutely loved everything that I’ve studied, and I’m already looking forward to next year, when I’ll be taking more specialized classes and fewer introductory/foundational advanced math courses. I think the wildest thing I’ve realized this year is looking back at August 2015, when I first got to Penn State and began working on qualifying exam prep, I had no idea what I was doing. I couldn’t answer almost any of the questions. But after working at them for so long, learning so much material this year, and spending the hours I’ve spent reading and learning and mastering new ideas, I can honestly tell how far I’ve come. It’s like when you’re hiking a mountain, you reach a ledge, you look out over the valley, and you see the trail head miles below you, and you think, “Holy crap, I started all the way back there??”
Plus, the feeling of finally being able to understand how to solve a problem never gets old:


You know how I mentioned those undergrad friends thinking of math grad school? At this point they’ve probably heard me complain about how stressed I am, but also how much I’ve loved being in grad school. I gotta say, I’m feeling much more of the latter. I can’t think of anything else I’d rather be doing than teaching, still learning, and beginning to think about research on the horizon. So to my undergrad math friends thinking of going on to grad school (you know who you are), stick with it. It’s incredibly difficult, but you’ll be amazed at how much you’ve learned at the end of your first year alone. Try getting your hands dirty with math research. If you like it, and if you can’t see the magic of mathematics ending any time soon (and trust me, it never ends), apply for grad school. You will be so glad you did.
As for my own research, originally I went into Penn State thinking I was going to research dynamical systems, and I may still. But I’m open to studying other things as well; after this differentiable manifolds course I took, I’m toying with the idea of going into something geometric or topological. I’m taking a course next year in algebraic topology and a topics course in twisted K-theory, so those might inform me if this is something worth exploring. But either way, I won’t really be able or ready to start getting involved in research until I’m done with qualifying exams.
I should probably explain what these “qualifying exams” are. The quals are a sequence of four exams in four different areas of mathematics. There are six different exams, two of which are mandatory, and the other two you choose from the remaining four. Each exam has four questions; you have to answer two of them almost perfectly within two hours. I’m gonna do my best to explain what the four exams I took were loosely about:

Linear Algebra: Stuff is really nice, and here’s how you can make it even nicer. You can’t always make it nice, but you usually can. You may not learn in class how to make it super nice, but you’re expected to know how to make it super nice on your own. Imagine those planes on the right, in 21 dimensions. Just make sure you know how to really make it extra specially super nice, no matter what they throw at you. Because God knows what they'll throw at you (hey, grad school was never supposed to be easy).

Real Analysis: Stuff is not nice (that scribbly line is called a "Devil's Staircase," with good reason). Essentially everything you learned in calculus is a lie. Here’s how things really work. You’ll never be able to compute anything, and when you do need to compute something, the old way is good enough, even though it’s a lie. You’ll be tempted to draw lots of pictures; your own pictures will often be the biggest lies. Basically trust nothing.

Complex Analysis: You do calculus with complex numbers. You can't graph complex functions (they're 4-dimensional graphs), but the thing on the right comes pretty close. And it’s really awesome. It’s so incredibly pretty. But it’s calculus, and you learned in Real Analysis that calculus is a lie, and you may have some existential crises as a result. Just roll with it.
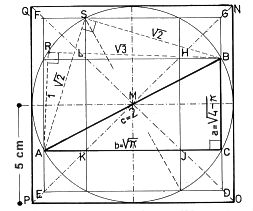
Abstract Algebra: Groups, rings, modules, fields. Geometric quandries, like the one on the left (here's what they're doing). It has the possibility to make really pretty pictures even prettier, but you don’t see any of those pictures. Numbers make a lot more sense. Also you learn about a dude who turned mathematics on its head and proceeded to get shot in a duel the next day for what may or may not have been a really dumb reason. You might say he threw away his shot.
So that’s what the exams were about. (Explaining what they’re actually about is really difficult but hit the links and message me if you’re curious!) Words cannot express how it feels to take a qualifying exam, but it's something like...

The complex analysis and abstract algebra exams at PSU are generally more predictable. Linear algebra has become really tricky in recent years. Real analysis hands down is the least predictable. That exam can have some of the toughest questions with surprisingly easy answers, provided you either (a) can see the solution in juuuuust the perfect way, or (b) have done a hundred problems similar to the one you're working on. And I knew that my solutions to the real analysis qual were seriously lacking, even as I walked out of the exam room.
You have no earthly idea how happy I was when I found out that I passed real analysis this semester.

I passed complex and abstract as well, so just linear algebra left!
Since the end of this past semester, I’ve been studying like crazy for linear, getting ready to take it again next December. I’ve solved every problem from the qualifying exams from Fall 2008 to today. Next up: tackle the quals from 1992 to 2007. I’m planning on looking at qualifying exams from Berkeley and U. Michigan as well. Anyone else have other suggestions for good linear problems?
The other courses this semester I took were point-set topology (the subject of that class is gonna be a future post), introduction to algebraic number theory, and differentiable manifolds. The number theory class I mostly took because I was curious about the subject; I have many friends at PSU and other places who have done work in number theory and really enjoyed it, so I thought I’d check it out. As much as I loved the professor for the course (who was also my abstract algebra professor), I don’t think algebraic number theory is for me. Although I kind of regret taking the number theory class before abstract algebra, and not the other way around. Differentiable manifolds is not a qualifying exam course (thank God because it’s incredibly weird), but it’s still one of these fundamental mathematics courses that every researcher needs to know a little bit about. It’s another way to generalize calculus by doing calculus on spheres, tori, Möbius strips, Klein bottles, or higher dimensional manifolds, as opposed to just doing calculus on a line, or on a plane. (And if you want to try visualizing what that might look like, you may need a controlled substance to assist you.) As much as I enjoyed this class, it became progressively more difficult to understand what was going on, especially as I spent more time studying for qualifying exams and less time focusing on my courses. (An unfortunate but ultimately necessary tradeoff.)
I’m planning on spending at least some time this summer studying up on differentiable manifolds and filling in the blanks. People have recommended I read through John Lee’s textbook on smooth manifolds and Michael Spivak’s book on differential geometry. Professor Ping Xu at Penn State recommended I take a look at a book on Lie theory as well, for his topics course on twisted K-theory. As much as I’d rather be reading those books, I do have to study for linear algebra as well… and I’ll likely be doing way more of the latter. (Anyone know a good way to strike a balance?)
Being a mathematics Ph.D. student is a little like being a Jedi in training. You start out thinking you know what your training will entail, and what you will do once you complete your training, but you’re usually wrong about both. Your professors warn you about all the strange aspects of the mathematical universe, how challenging real mathematics research is, and naïvely you tell them, “I’m not afraid!” But like Yoda on Dagobah, they tell you again and again, “You will be.” You have a massively difficult task ahead of you, and you face failure several times in different ways before finally overcoming the myriad challenges your program hurls at you. Quals are the first one, but there will be others: comprehensive exams, fellowship applications, publications, and of course, the dissertation defense. But you need to face failure in order to succeed. And if afterwards you can find a way to stand up, still hear the universe call your name, understand how far you still have to climb, and still find your voice to honestly cry out, “I am not afraid,” then succeed you will.
Succeed I will.




Comments